コンボリューション逆投映法(CBP法)
コンボリューション補正逆投影法、もしくはコンボリューション逆投影法(CBP : Convolution Back Projection)は、逆投影が作るボケの補正に相当する操作を、投影データに対して事前に施す方法です。まず、ある定められた補正関数(コンボリューション関数) \(h\) と投影データをコンボリューション(畳み込み積分)することで、補正済み投影データ \(\hat{p}\) を得ます。\(\hat{p}\) は 投影データ \(p(X,\theta )\) と補正関数 \(h(X)\) を用いて、次のように表されます。
$$ \hat{p}(X,\theta) = p(X,\theta) \ast h(X) = \int_{-\infty}^{\infty}h(X-X’)p(X’, \theta) dX’ $$
補正済みの投影データ \(\hat{p}\) を逆投影することで、ボケの無い再構成画像を得ることができます。コンボリューション関数と呼ばれる関数 \(h\) の基本形状は、中央がデルタ関数的な正値、左右が負の値で \(0\) に漸近しており、波形積分値が \(0\) というものになります。これは、遠くまで伸びたボケを補正するデコンボリューションの関数形であることを意味します。コンボリューション関数 \(h\) の具体例として、Ramachandran と Lakshminaraynan による \(h_{\rm RL}\) を以下に示します。
$$h_{\rm RL}(X) = h(n\cdot \Delta X) =\begin{cases} -\displaystyle\frac{1}{2}\frac{1}{\pi^2 \cdot \Delta X^2 \cdot n^2} & (n = {\rm odd})\\ 0 & (n = {\rm even}) \end{cases} $$
また、Shepp と Logan による \(h_{\rm SL}\) を以下に示します。
$$ h_{\rm SL}(X) = h(n\cdot \Delta X) = -\frac{4}{\pi}\frac{1}{\Delta X^2}\frac{1}{4n^2-1} $$
多くの CT装置では、これらのコンボリューション関数が用いられます。実際に、コンボリューション関数 \(h_{\rm SL}\) を用いると投影データがどのようになるのか、見てみましょう。前節で得た、0,10,0 の投影データに対してのコンボリューション結果は次のようになります。
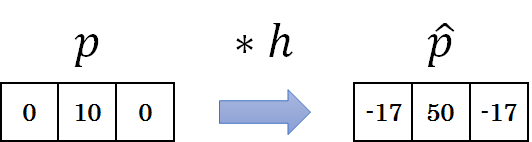
このように、投影データはコンボリューションによって正値の両端がえぐれたような形となります。このエグレが逆投影によるボケと互いに相殺することで、エッジの強調された理想的な再構成画像を得ることができます。実際に、補正済みの投影データを空画像に対して逆投影していく様子を見てみましょう。
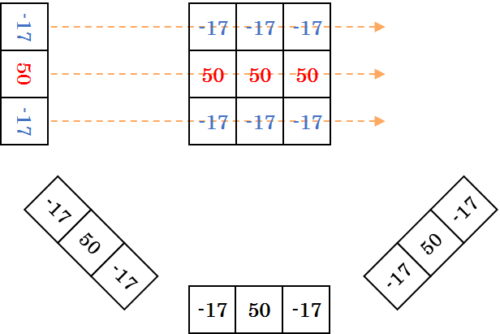
まずは左から右方向へ、逆投影します。
続いて、左下方向から右上方向への逆投影です。
下方向から上方向への逆投影です。
最後に、右下方向から左上方向への逆投影です。
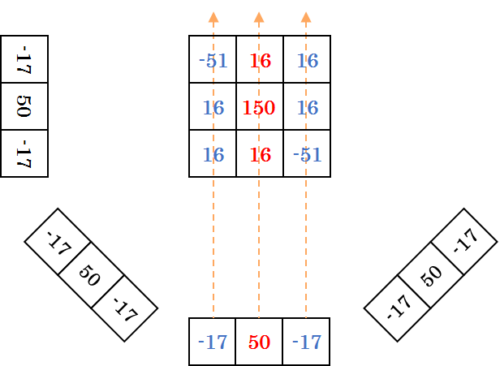
中央の値は増加していき \(200\) となっていますが、周囲の値は正の値と負の値で相殺され、最終的には \(-1\) となっています。
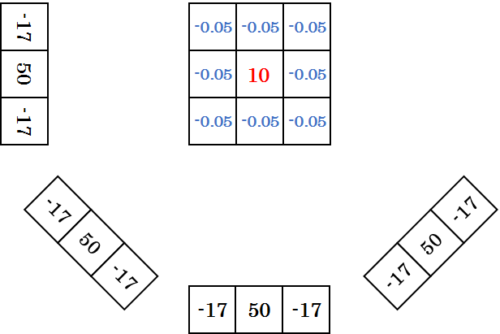
中央の値が \(10\) になるように全体をスケーリングすると、周囲の値は \(-0.05\) となり、ほぼ元の数値ファントムを再現することに成功しています。このように、投影データに対してコンボリューション補正を行うことで逆投影時の画像のボケを消すことが、コンボリューション逆投影法の概要です。ここでは、数式の詳説は割愛します。