本節では、X線CT の画像再構成法の中で最も単純な方法である、単純逆投影法(SBP : Simple back projection)を説明します。
投影のモデル化
単純逆投影法を説明する上で、まずは順投影のモデル化を行います。
入射X線強度を \(I_{\rm in}\)、透過X線強度を \(I_{\rm out}\)、2次元のX線吸収係数の分布を \(\mu(x,y)\),\(x\)-\(y\) 座標系を \(\theta\) だけ回転させた座標系を \(X\)-\(Y\) 座標系とすると、順投影は次の式によって表されます。
$$ I_{\rm in}(X,\theta) = I_{\rm out} \exp\left( – \int_{-\infty}^{\infty} \mu(x,y) dY \right) $$
また、\(I_{\rm in}\) が既知であることから、投影データ \(p\) は上式を変形して次のように表されます。
$$ p(X,\theta) = \int_{-\infty}^{\infty} \mu(x,y) dY $$
この式は \(\mu(x,y)\) を \(Y\) 軸に沿って線積分した形になっており、この変換はラドン変換と呼ばれます。
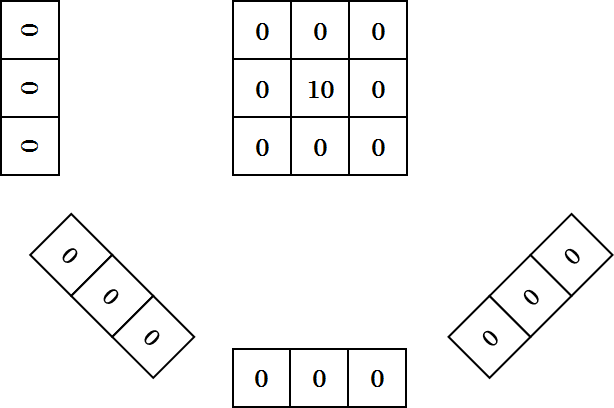
順投影計算を、簡単なモデルを使って説明します。下の図は、中心にだけ(X線吸収係数が \(10\) の)物体が存在する、\(3\times 3\) の仮想的な断面を表しています。このような仮想的な断面は、数値ファントムと呼ばれます。また、数値ファントムの周囲にある \(3\times 1\) の数値の列は、各方向から X線を照射した際に検出器が出力する値(投影データ)を意味します。
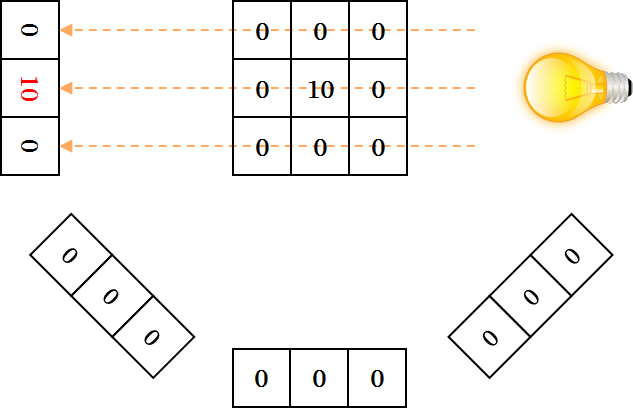
実際に、右方向に X線源を置き、左方向に X線を照射した場合を考えてみましょう。投影データは、通過した物体の X線吸収係数の積分によって表されるので、下に示す図のように中央の検出素子のみが 10 という値を出力することがわかります。
同様にして、周囲方向から X線を照射していくと、下の図のようになります。ここでは簡単のため、0、45、90,135度の 4 方向から投影データを収集しています。
この数値ファントムは回転対称な図形なため、どの方向から X線を照射しても、同じ投影データの列が得られることがわかります。以下では、順投影によって得られたこの投影データを逆投影していくことを考えます。
単純逆投影法
単純逆投影法(SBP : Simple Back Projection)とは、撮影で得た投影データを計算機上の空画像へ向かって、直前状に投影データを加えていく操作のことを指します。上で示したようなパラレルビームの投影データが半回転にわたってあるとすると、単純逆投影法で作られる画像 \(\mu_{\rm SBP}(x,y)\)は、次の積分式で表されます。
$$ \mu_{\rm SBP}(x, y) = \frac{1}{\pi}\int_{0}^{\pi} p(X, \theta) d\theta $$
この式は、点\( (x,y)\)における画素値は、その点を通る全方向からのレイの値を足したものであることを意味します。投影データを得たプロセスを逆に辿ること、すなわち、投影データの値を投影方向に沿って画像に足しこんでいく操作が逆投影です。
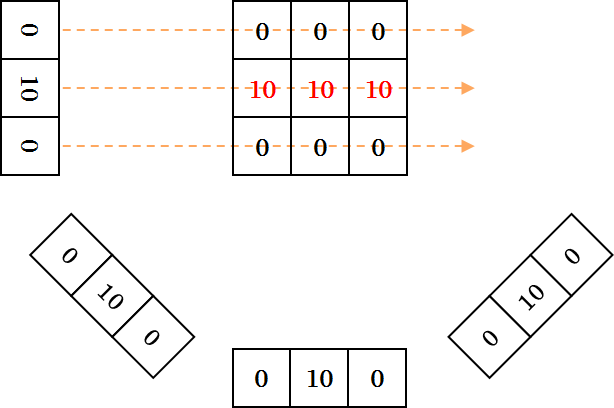
実際に、先ほどと同じ簡単なモデルを使って、逆投影の様子を見てみましょう。左方向から右方向に向けて逆投影をすると、以下のようになります。投影データが直線状に加えられていくことがわかります。
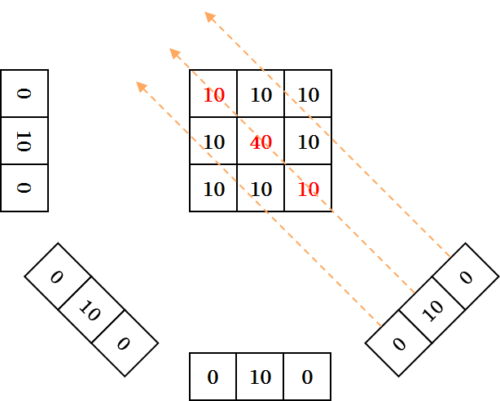
さらに、4 方向から逆投影を行うと、以下のようになります。中央が \(40\) で、その周囲が \(10\) という数字になっています。
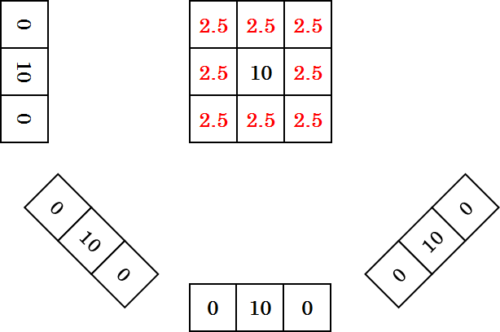
最後に、4 方向からの投影データを重ねあわせたので、4 という数字で除します。結果、以下のようになります。
中央が \(10\) で、その周囲が \(2.5\) となりました。中央のみは、元の数値ファントムの \(10\) という値を再現できていますが、その周囲は元々 \(0\) だったのにも関わらず \(2.5\) と間違った値となりました。これを画像化すると、中央が白く、周りがグレーのぼやけた画像になります。このように、単純逆投影法は再構成画像にボケを発生させてしまいます。
また、上では \(3\times 3\) の画像解像度での説明を行いましたが、もっと大きい画像で投影方向数も多くしたケースを考えてみましょう。そのような場合、デルタ関数的な投影データは、各方向からの逆投影ごとに一本のスポーク状のデータを再構成画像上に描くことになります。それを画像化すると、以下のようになります。
このスポークの密度は、中心の点からの距離に反比例したものになっており、この連続的な密度の変化が逆投影の作るボケとなっています。一方、このような数学的挙動がはっきりしているボケであれば、それを解消することは可能であり、その代表的な方法としてコンボリューション補正やフィルタ補正があります。次節以降では、これらについて解説をしていきます。